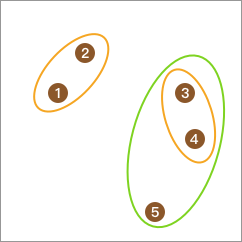
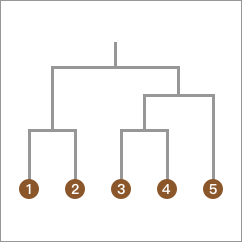
DBSCAN (Density-Based Spatial Clustering of Applications with Noise) 是一种基于密度的聚类算法,基于密度的聚类寻找被低密度区域分离的高密度区域。常用于异常值或者离群点检测。
DBSCAN 怎么算
当某个点的密度达到算法设定的阈值,则这个点称为核心对象。(即r领域内点的数量小于minPts),其中领域的距离阈值为用户设定值。
若某点p在q的r领域内,且q是核心点,则p-q直接密度可达。若有一个点的序列q0、q1、q2…qK,对任意的qi-qi+1是直接密度可达的,则称q0到qK密度可达。称为密度的传播。
当一个非核心点不能发展下线,则称该点为边界点。若某一点,从任一核心地点出发都是密度不可达的,则称该点为噪声点
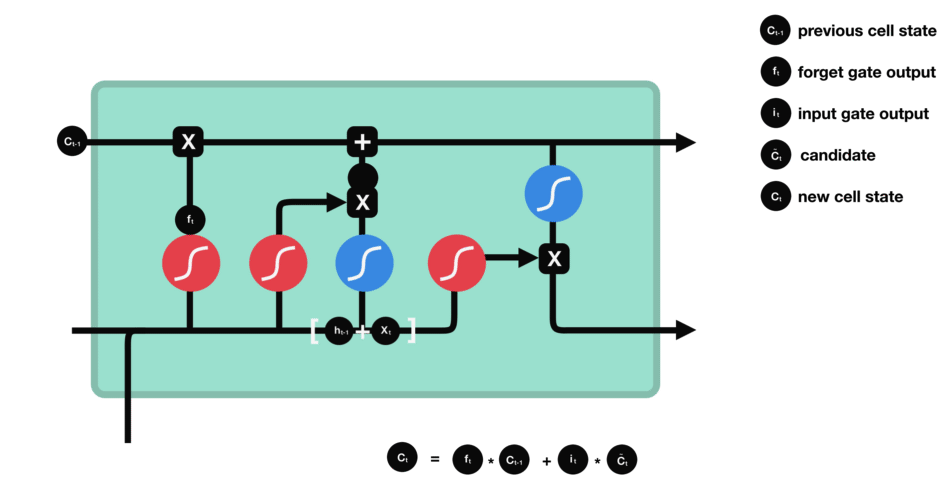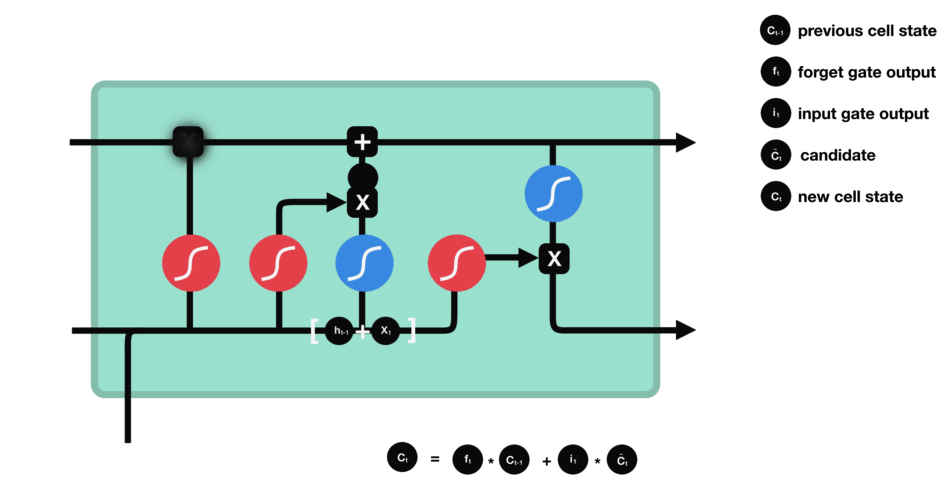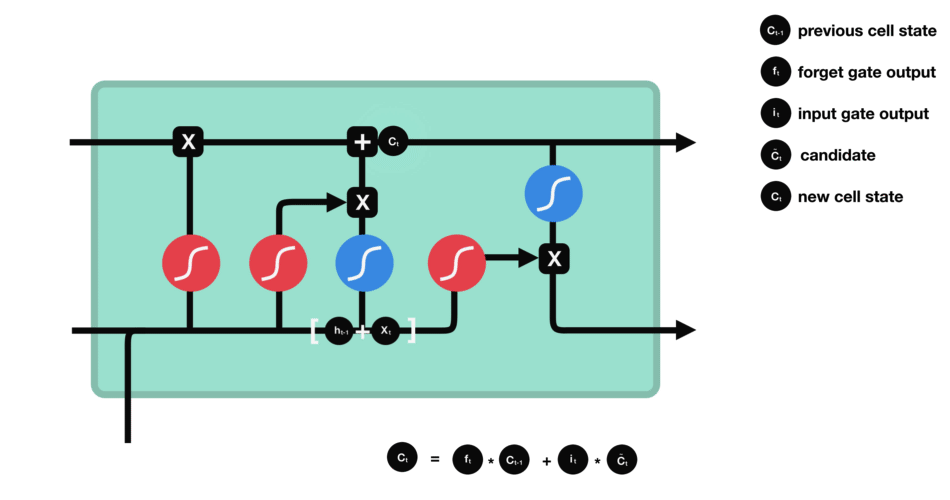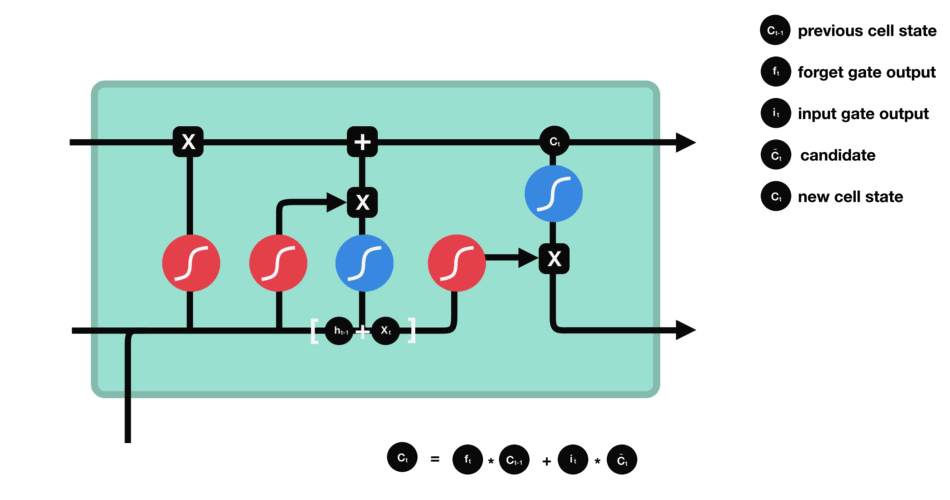
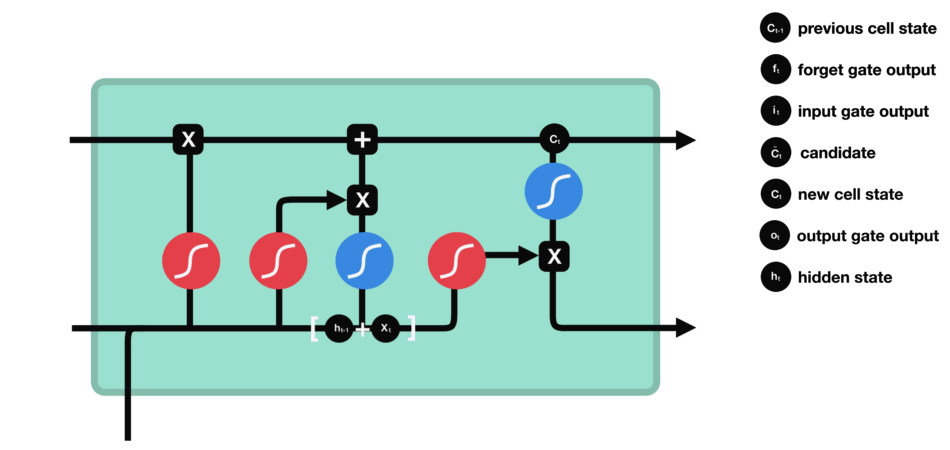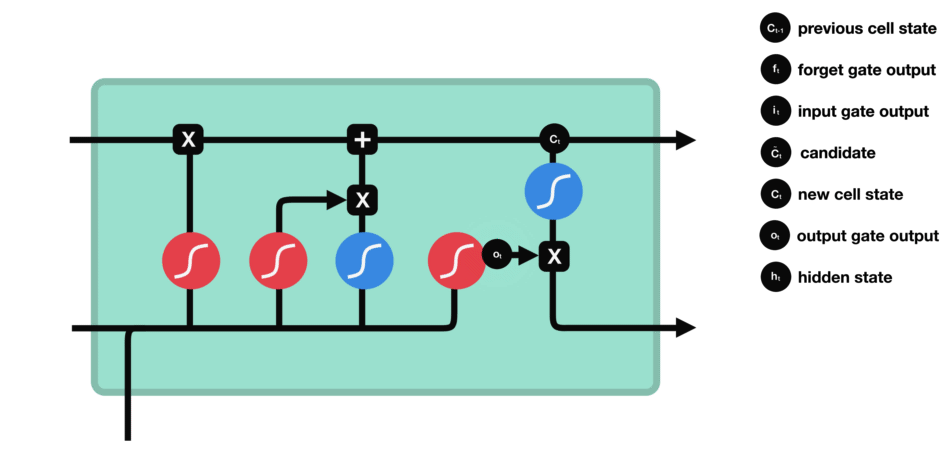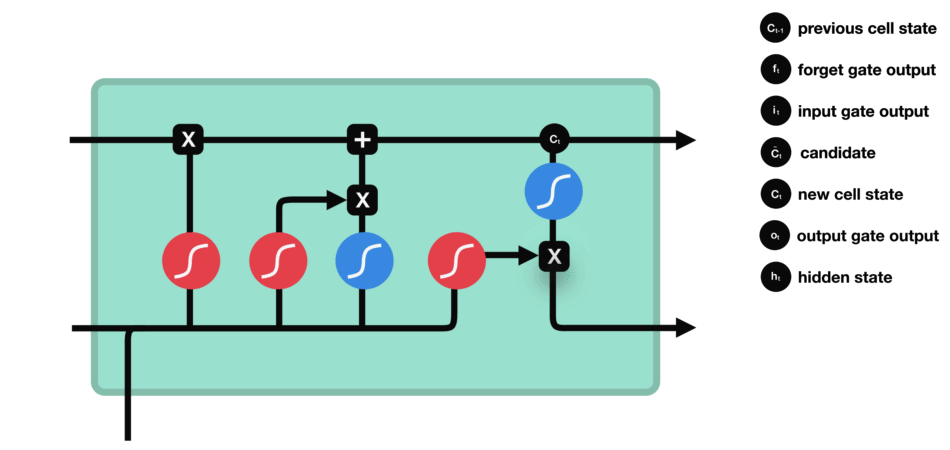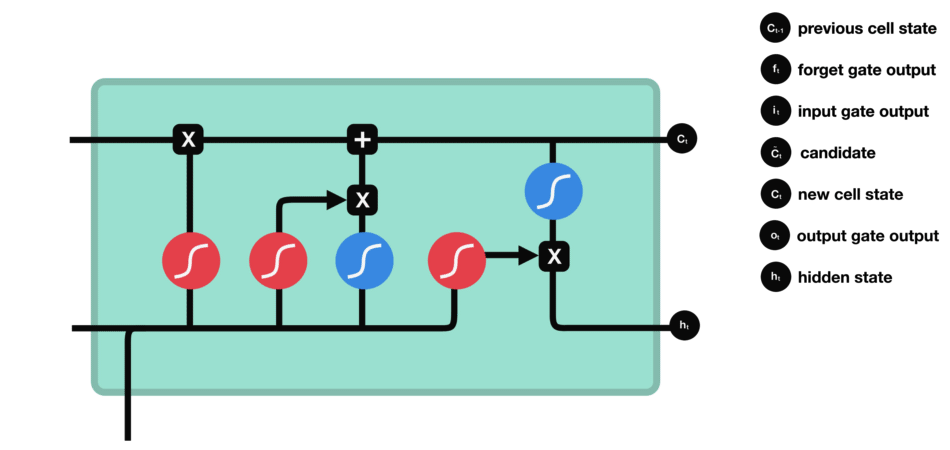
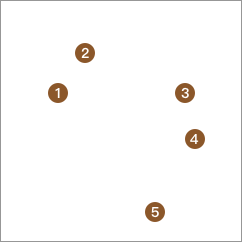
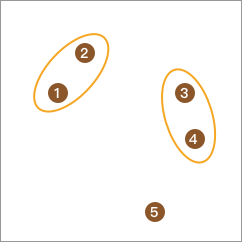
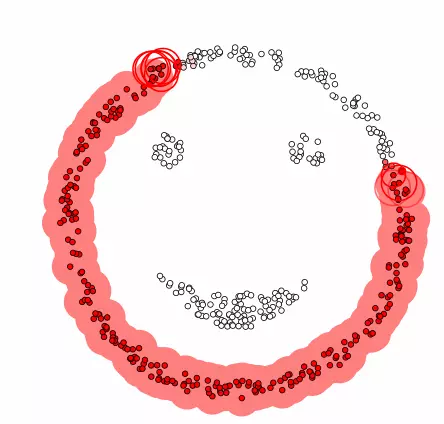
DBSCAN 聚类算法实现如下图:
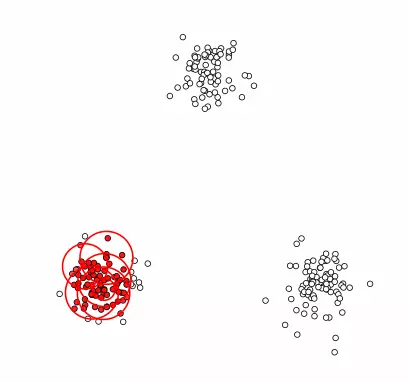
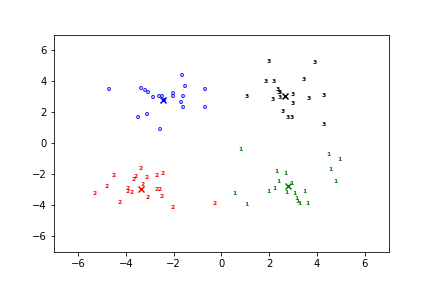
当出现奇葩数据时,K-Means 无法正常聚类,而 DBSCAN 完全无问题
优点:
-
与K-Means相比,不需要手动确定簇的个数K,但需要确定邻域r和密度阈值minPts
-
能发现任意形状的簇
-
能有效处理噪声点(邻域r和密度阈值minPts参数的设置可以影响噪声点)
缺点:
-
当数据量大时,处理速度慢,消耗大
-
当空间聚类的密度不均匀、聚类间距差相差很大时参数密度阈值minPts和邻域r参数选取困难
-
对于高维数据,容易产生“维数灾难”(聚类算法基于欧式距离的通病)
DBSCAN 聚类 Python 实现
# coding=utf-8
"""
Created on 2019/10/12 11:42
@author: EwdAger
"""
import numpy as np
from sklearn.cluster import DBSCAN
from sklearn import metrics
from sklearn.datasets.samples_generator import make_blobs
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
centers = [[1, 1], [-1, -1], [1, -1]] # 生成聚类中心点
X, labels_true = make_blobs(n_samples=750, centers=centers, cluster_std=0.4,random_state=0)
# 生成样本数据集
X = StandardScaler().fit_transform(X)
# StandardScaler 标准化处理。且是针对每一个特征维度来做的,而不是针对样本。
# 调用密度聚类 DBSCAN
db = DBSCAN(eps=0.3, min_samples=10).fit(X)
# print(db.labels_) # db.labels_为所有样本的聚类索引,没有聚类索引为-1
# print(db.core_sample_indices_) # 所有核心样本的索引
core_samples_mask = np.zeros_like(db.labels_, dtype=bool) # 设置一个样本个数长度的全false向量
core_samples_mask[db.core_sample_indices_] = True #将核心样本部分设置为true
labels = db.labels_
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
# 获取聚类个数。(聚类结果中-1表示没有聚类为离散点)
# 模型评估
print('估计的聚类个数为: %d' % n_clusters_)
print("同质性: %0.3f" % metrics.homogeneity_score(labels_true, labels)) # 每个群集只包含单个类的成员。
print("完整性: %0.3f" % metrics.completeness_score(labels_true, labels)) # 给定类的所有成员都分配给同一个群集。
print("V-measure: %0.3f" % metrics.v_measure_score(labels_true, labels)) # 同质性和完整性的调和平均
print("调整兰德指数: %0.3f" % metrics.adjusted_rand_score(labels_true, labels))
print("调整互信息: %0.3f" % metrics.adjusted_mutual_info_score(labels_true, labels))
print("轮廓系数: %0.3f" % metrics.silhouette_score(X, labels))
# Plot result
unique_labels = set(labels)
colors = [plt.cm.Spectral(each) for each in np.linspace(0, 1, len(unique_labels))]
plt.figure(figsize=(10,6))
for k, col in zip(unique_labels, colors):
if k == -1: # 聚类结果为-1的样本为离散点
# 使用黑色绘制离散点
col = [0, 0, 0, 1]
class_member_mask = (labels == k) # 将所有属于该聚类的样本位置置为true
xy = X[class_member_mask & core_samples_mask] # 将所有属于该类的核心样本取出,使用大图标绘制
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col), markeredgecolor='k', markersize=14)
xy = X[class_member_mask & ~core_samples_mask] # 将所有属于该类的非核心样本取出,使用小图标绘制
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col), markeredgecolor='k', markersize=6)
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()
输出